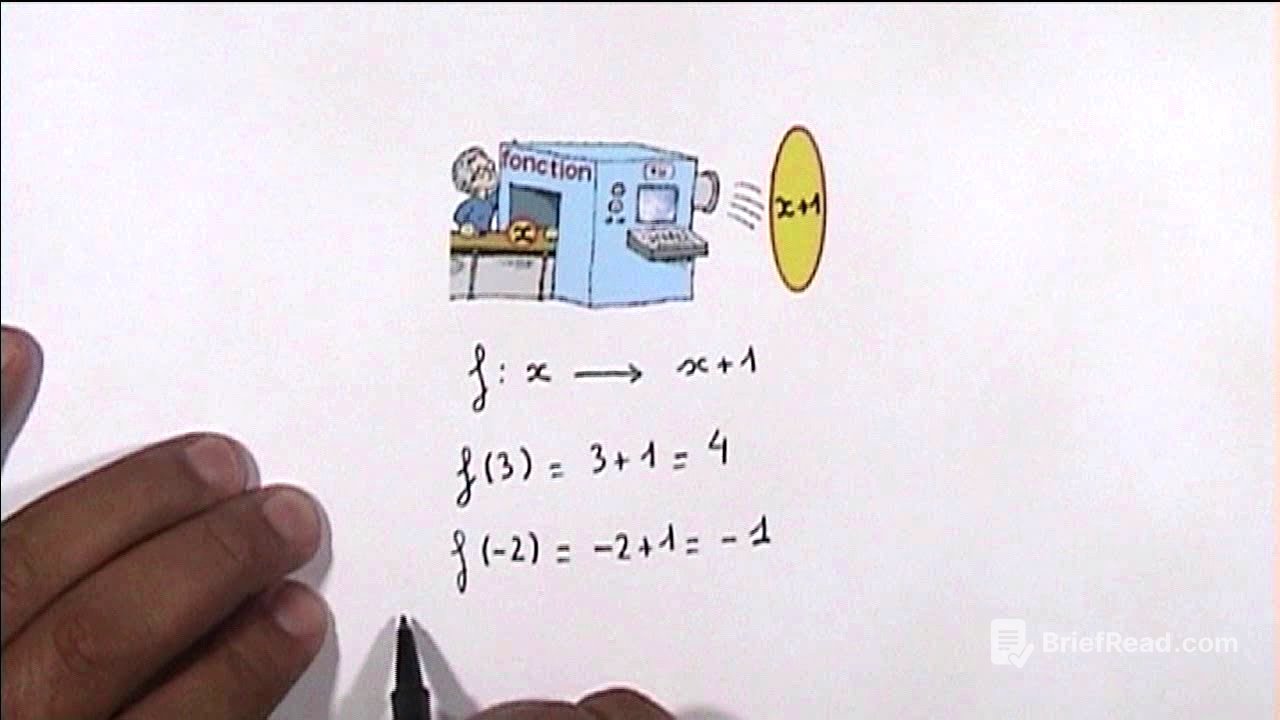Résumé
Cette vidéo explique le concept de fonction en mathématiques à l'aide d'une métaphore de machine qui transforme un nombre en un autre. Elle introduit la notation des fonctions, la notion d'image et d'antécédent, et montre comment représenter une fonction à travers un tableau de valeurs et un graphique. La vidéo utilise le logiciel GeoGebra pour visualiser des fonctions et identifier des formes de courbes comme la parabole.
- Introduction du concept de fonction comme une machine transformant des nombres.
- Explication de la notation des fonctions et des termes image et antécédent.
- Utilisation de tableaux de valeurs et de graphiques pour représenter des fonctions.
- Démonstration avec le logiciel GeoGebra pour visualiser et analyser des fonctions.
Introduction à la notion de fonction [0:01]
L'auteur introduit l'idée d'une machine qui transforme un nombre en un autre, par exemple, 2 devient 5 et 4 devient 9. Il explique qu'il peut créer un tableau de valeurs pour suivre les entrées et les sorties de cette machine. L'objectif est de perfectionner cette machine en lui donnant une instruction spécifique, comme ajouter 1 à chaque nombre entrant.
Définition mathématique d'une fonction [1:16]
L'auteur explique que cette machine est en fait une fonction mathématique, qui transforme un nombre en un autre selon un procédé donné. Il généralise le concept en utilisant la variable x pour représenter l'entrée de la machine, et x + 1 pour la sortie, dans le cas où la machine ajoute 1. Il nomme cette fonction "f" et la note f(x) = x + 1. Il explique que si on entre 3 dans la fonction, on obtient 4, et que 4 est l'image de 3 par la fonction f, tandis que 3 est l'antécédent de 4.
Nouvelle fonction et tableau de valeurs [5:31]
L'auteur introduit une nouvelle fonction, nommée G, qui associe à x la valeur x² + 1. Il calcule plusieurs valeurs de G pour différents nombres, comme G(-3) = 10 et G(-2) = 5. Il rappelle les notions d'image et d'antécédent dans le contexte de cette nouvelle fonction. Ensuite, il organise ces valeurs dans un tableau.
Représentation graphique d'une fonction [7:12]
L'auteur explique comment représenter les valeurs d'une fonction en utilisant un repère avec l'axe des abscisses (x) pour l'entrée et l'axe des ordonnées (y) pour la sortie. Il place plusieurs points sur le graphique en utilisant les valeurs calculées précédemment, comme (-3, 10) et (-2, 5). Il remarque que ces points semblent former une courbe régulière, appelée parabole. Il souligne que la forme de la courbe peut aider à identifier le type de fonction.
Visualisation avec GeoGebra [9:57]
L'auteur utilise le logiciel GeoGebra pour tracer les représentations graphiques des fonctions f(x) = x + 1 et g(x) = x² + 1. Il montre comment trouver l'image d'un nombre en utilisant le graphique, et comment identifier l'antécédent d'un nombre. Il superpose les deux courbes sur le même graphique et observe les points d'intersection, qui représentent les valeurs pour lesquelles les deux fonctions donnent la même image.
Détermination graphique de l'image et des antécédents [14:33]
L'auteur utilise GeoGebra pour déterminer graphiquement l'image et les antécédents d'une fonction définie par f(x) = 0.5x² - 2x. Il montre comment trouver l'image de 2 en traçant une ligne verticale à partir de x = 2 jusqu'à la courbe, puis en lisant la valeur de y correspondante. De même, il explique comment trouver les antécédents de 6 en traçant une ligne horizontale à partir de y = 6 jusqu'à la courbe, puis en lisant les valeurs de x correspondantes.
Récapitulation des concepts clés [17:20]
L'auteur récapitule les concepts clés de la vidéo, en rappelant qu'une fonction est comme une machine qui transforme un nombre en un autre. Il souligne que l'image est ce qu'on obtient à la sortie de la machine, et l'antécédent est le nombre qu'on a introduit dans la machine. Il utilise l'exemple de la fonction f(x) = x² + 1 pour illustrer ces concepts, et montre comment trouver l'image de 3 et de -2. Il explique que 5 a deux antécédents (2 et -2) par la fonction f, mais que l'image d'un nombre est unique.
Détermination d'une fonction par différentes méthodes [20:39]
L'auteur explique comment déterminer une fonction par différentes méthodes : par une formule littérale, par un graphique, ou par un tableau de valeurs. Il montre comment utiliser un graphique pour trouver l'image d'un nombre, et comment reconnaître des formes particulières de courbes, comme la parabole pour une fonction du type x² + 1. Il explique comment utiliser un tableau de valeurs pour tracer la courbe d'une fonction, en plaçant les points correspondants et en reliant les points pour obtenir la forme de la courbe.